Found a pic of me without my name on it :)
Anyway, it is good.
http://crossroads.newsworks.org/index.php/local/keystone-crossroads/75889-robot-could-make-bridge-inspections-quicker-and-easier
3/28/2016
9/26/2011
Solve the Traveling Salesman Problem (TSP) by Simulated Annealing (SA)
1.
Objective
The objective
of this work is developing a generic simulated annealing (SA) algorithm to
solve the traveling salesman problem (TSP), which is find the shortest route
through N given cities such that every city is visited exactly once.
2.
Concepts and Programming
Simulated
annealing algorithm, first described by
Scott Kirkpatric [2], has its name and inspiration come
from annealing in metallurgy, a technique involving heating and slowly
cooling of a material to increase physical strength and/or reduce defects. When
the temperature is hot, the atoms of the material piece gain high
energy and wander randomly. The slow cooling gives them more chances of finding
configurations with lower internal energy than the initial one [3]. In term of
an optimization algorithm, each step of the SA algorithm replaces the current
solution by a random "neighbor" solution, chosen with a probability
that depends both on the difference between the corresponding function values
(energy) and also on a global parameter T (called
the temperature). The temperature is gradually decreased during the
process. At the beginning, T is large, the "upnhill" moves
(go to higher energy states) are more likely accepted than when T is go to zero
at the end of the process. This allows the SA algorithm move out of the local
minimum at the early states.
Table 1: Pseudo
code of SA algorithm [2]
s ← s0; // Initial state, energy.
e ← E(s)
sbest ← s; // "best"
solution
ebest ← e
k ← 0
while k < kmax and e > emax
// Trail move to ‘ neighbor’
snew ← neighbor(s)
enew ← E(snew)
// Accept uphill move if ‘feel lucky’
if
P(e, enew, temp(k/kmax)) > random() then
s ← snew;
e ← enew; end // Tracking the best-ever
if enew < ebest then
sbest ← snew;
ebest ← enew end
k ← k + 1
return sbest
|
There are different schemes to accept the “uphill”
move as well as to reduce the temperature, such as Fast Cauchy, Geometric, or
Boltzmann’s methods as given in [1]- lecture 3, page 5.
Actually, the "pure" SA algorithm as
described in [1] does not keep track of the best solution found so far: it does
not use the variables sbest and ebest, it lacks the
second if inside the loop, and, at the end, it returns the current
state s instead of sbest. While remembering the best state is a
standard technique in optimization that can be used in any meta-heuristic, it
does not have an analogy with physical annealing — since a physical system can
"store" a single state only.
In TSP problem:
- Each state “s” is represented by a combinatory of N
cities’ indexes.
- The energy E(s) is a function to compute the total
travel distance of visiting N cities following the route or the state s.
- The initial sate or route s is selected randomly.
- The “neighbor” of s is implemented by swapping 2
random cities of the route s. There are 2 ways to swap: swap the two vertices
or swap the two edges as described in [1]-lecture 3, page 17, and are both
implemented in my code (See Code listing section)
- The probability to accept a move is P = exp(- DE/kT) = exp(-(enew-e)/kT)
- Update temperature T = αT, where 0<α<1
3. Some Results
 |
| SA process |
 |
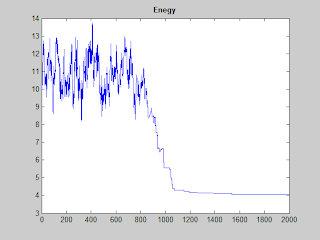| The convergence of SA |
 |
| GUI (Graphic User Interface) written in Matlab |
http://www.mathworks.com/matlabcentral/fileexchange/9612-traveling-salesman-problem-tsp-using-simulated-annealing . So what the difference?
Main thing is the speed. I am inspired by his work, but after downloaded, I found that his program could take "forever" for 101 cities. Could not sit and wait, (not a patient person) so I wrote this program. Most of the time, it just needs less than 10 seconds for 101 cities (including time for plot). For 500 cities, it may take 1 minutes.
Next time, I will upload the code and talk about using SA for solving N-Queens problem.
References
1.
Gary Yen. ECEN
5773 Intelligent Systems- Fall 2011 lecture notes. Oklahoma State University,
2011
2. Kirkpatrick, S., C. D.
Gelatt Jr., M. P. Vecchi, "Optimization by Simulated Annealing",Science, 220, 4598, 671-680, 1983.
9/17/2011
Pair-wise Weighted Euclidean distance between 2 sets of vectors
In many tasks, we wish compute the pair-wise distance between two sets of vectors (in high p-dimension space). For example, in clustering problem we want to compute the distance between each point in the given set of N points (or vectors), represent by a matrix X of size N-by-p, to every other points. The simplest implementation in Matlab may look similar to this:
DD = zeros(N,N);
for i =1:N
for k=1:N
DD(i,k) = sum((X(k,:)-X(i,:)).^2);
end
end
(It actually compute the SQUARE of the distance, but in many case it is enough, e.g for just want to know which is the nearest point to a given point; otherwise we can easy say DD=sqrt(DD). Compute the square distance is significantly faster)
However, as you know, using FOR loop in Matlab is so slooow. People said "Avoid FOR loop as much as possible".
By the way, the square Euclidean distance between two vector a and b is: d = sum((a-b).^2); and the weighted version is simply: d = sum(wts.*(a-b).^2).
The inner for-loop in the above code can be easily eliminated, such as:
DD = zeros(N,N);
for i =1:N
% inner for-loop of above code equivalent to:
DD(i,:) = sum((X - repmat(X(i,:),N,1)).^2);
end
But we still need the outer for-loop. How about get rid all of it? YES, it is possible. We just need a small trick:
(a-b)^2= a^2+b^2-2ab
Yes it is easy for 2 vectors, but applying for two matrix A and B need quite an arrangement.
Check out the following code:
%***************************
function DD = pdist2(A,B,Wts)
% Find pair-wise SQUARE EUCLIDEAN distance
% or 'Weighted square euclidean' distance
% between each point in A and B
% For 2 vector a, b
% Euclidean distance= d = sum((a-b).^2)
% Weighted version = d = sum(wts.*(a-b).^2)
% ------------------------------
% Input:
% A= m_by_p, m points in p-dimension
% B= n_by_p, n points in p-dimension
% Wts = 1_by_p, defaut = [1 1 ...]
% Results:
% DD= m_by_n
% ------------------------------
% Facts: (a-b)^2= a^2+b^2-2ab
% ------------------------------
% trungd@okstate.edu, Feb 2011
% ------------------------------
% Ideal from: Piotr Dollar. [pdollar-at-caltech.edu]
[m,p1] = size(A); [n,p2] = size(B);
if(p1~=p2) % check size
error('Must have: ncol(X)=ncol(Y)=length(Wts)')
end
if nargin < 3 % standard euclidean
AA = sum(A.*A,2); % column m_by_1
BB = sum(B.*B,2)'; % row 1_by_n
DD = AA(:,ones(1,n)) + BB(ones(1,m),:) - 2*A*B';
else
if p1 ~=length(Wts)
error('Must have: ncol(X)=ncol(Y)=length(Wts)')
end
sW = sqrt(Wts(:)'); % make sure row, square of Wts
A = sW(ones(1,m),:).*A;
B = sW(ones(1,n),:).*B; % modify A,B
% Process the same as standard Euclidean
AA = sum(A.*A,2);
BB = sum(B.*B,2)';
DD = AA(:,ones(1,n)) + BB(ones(1,m),:) - 2*A*B';
end
%***************************
It runs fast, just for the record my laptop is average, not supper:
>> A = rand(1000,100);
>> B = rand(2000,100);
>> W = rand(1,100);
>> tic, D = pdist2(A,B,W);toc
Elapsed time is 0.101665 seconds.
As said, the idea is from Piotr Dollar. [pdollar-at-caltech.edu], I modified to handle the weighted euclidean case (which I meet pretty offen).
Other type of distance such as Cosine, L1, Mahalanobis, ... can be handled, but some of them are not that handy.
Last thing, pdist2() is available in Statistic Toolbox of Matlab that can deal with much more general distance. If you have that toolbox, forget about the code here :)
DD = zeros(N,N);
for i =1:N
for k=1:N
DD(i,k) = sum((X(k,:)-X(i,:)).^2);
end
end
(It actually compute the SQUARE of the distance, but in many case it is enough, e.g for just want to know which is the nearest point to a given point; otherwise we can easy say DD=sqrt(DD). Compute the square distance is significantly faster)
However, as you know, using FOR loop in Matlab is so slooow. People said "Avoid FOR loop as much as possible".
By the way, the square Euclidean distance between two vector a and b is: d = sum((a-b).^2); and the weighted version is simply: d = sum(wts.*(a-b).^2).
The inner for-loop in the above code can be easily eliminated, such as:
DD = zeros(N,N);
for i =1:N
% inner for-loop of above code equivalent to:
DD(i,:) = sum((X - repmat(X(i,:),N,1)).^2);
end
But we still need the outer for-loop. How about get rid all of it? YES, it is possible. We just need a small trick:
(a-b)^2= a^2+b^2-2ab
Yes it is easy for 2 vectors, but applying for two matrix A and B need quite an arrangement.
Check out the following code:
%***************************
function DD = pdist2(A,B,Wts)
% Find pair-wise SQUARE EUCLIDEAN distance
% or 'Weighted square euclidean' distance
% between each point in A and B
% For 2 vector a, b
% Euclidean distance= d = sum((a-b).^2)
% Weighted version = d = sum(wts.*(a-b).^2)
% ------------------------------
% Input:
% A= m_by_p, m points in p-dimension
% B= n_by_p, n points in p-dimension
% Wts = 1_by_p, defaut = [1 1 ...]
% Results:
% DD= m_by_n
% ------------------------------
% Facts: (a-b)^2= a^2+b^2-2ab
% ------------------------------
% trungd@okstate.edu, Feb 2011
% ------------------------------
% Ideal from: Piotr Dollar. [pdollar-at-caltech.edu]
[m,p1] = size(A); [n,p2] = size(B);
if(p1~=p2) % check size
error('Must have: ncol(X)=ncol(Y)=length(Wts)')
end
if nargin < 3 % standard euclidean
AA = sum(A.*A,2); % column m_by_1
BB = sum(B.*B,2)'; % row 1_by_n
DD = AA(:,ones(1,n)) + BB(ones(1,m),:) - 2*A*B';
else
if p1 ~=length(Wts)
error('Must have: ncol(X)=ncol(Y)=length(Wts)')
end
sW = sqrt(Wts(:)'); % make sure row, square of Wts
A = sW(ones(1,m),:).*A;
B = sW(ones(1,n),:).*B; % modify A,B
% Process the same as standard Euclidean
AA = sum(A.*A,2);
BB = sum(B.*B,2)';
DD = AA(:,ones(1,n)) + BB(ones(1,m),:) - 2*A*B';
end
%***************************
It runs fast, just for the record my laptop is average, not supper:
>> A = rand(1000,100);
>> B = rand(2000,100);
>> W = rand(1,100);
>> tic, D = pdist2(A,B,W);toc
Elapsed time is 0.101665 seconds.
As said, the idea is from Piotr Dollar. [pdollar-at-caltech.edu], I modified to handle the weighted euclidean case (which I meet pretty offen).
Other type of distance such as Cosine, L1, Mahalanobis, ... can be handled, but some of them are not that handy.
Last thing, pdist2() is available in Statistic Toolbox of Matlab that can deal with much more general distance. If you have that toolbox, forget about the code here :)
11/21/2010
How to draw a multivariable Gaussian random variable?
% Create Gaussian d-dimensional random variable
% Using Cholesky factorization
% Input:
% mu: mean vector, d-by-1
% cov: covariance matrix, positive definite, d-by-d
% n: number of samples, =100 default
% Output:
% X: d-by-n, each column is a sample
%-------------------
% trungd@okstate.edu
% Example
% x = gauss_d;
% y = gauss_d([0;5],[1 .9;.9 1],200);
% figure, hold on
% scatter(x(1,:),x(2,:))
% scatter(y(1,:),y(2,:))
function X = gauss_d(mu,covm,n)
if nargin<3, n=100;end
if nargin<2, covm=[1 0;0 1]; end
if nargin<1, mu=[0 0]; end
% -------------------
% Better to check size of mu, covm here
% I am lazy to do that :)
% -------------------
mu = mu(:)'; % make sure be row
d = length(mu);
% Get Cholesky factorization of covariance.
R = chol(covm);
% Generate the standard normal random variables.
Z = randn(n,d);
X = Z*R + repmat(mu,n,1);
X = X';
% Using Cholesky factorization
% Input:
% mu: mean vector, d-by-1
% cov: covariance matrix, positive definite, d-by-d
% n: number of samples, =100 default
% Output:
% X: d-by-n, each column is a sample
%-------------------
% trungd@okstate.edu
% Example
% x = gauss_d;
% y = gauss_d([0;5],[1 .9;.9 1],200);
% figure, hold on
% scatter(x(1,:),x(2,:))
% scatter(y(1,:),y(2,:))
function X = gauss_d(mu,covm,n)
if nargin<3, n=100;end
if nargin<2, covm=[1 0;0 1]; end
if nargin<1, mu=[0 0]; end
% -------------------
% Better to check size of mu, covm here
% I am lazy to do that :)
% -------------------
mu = mu(:)'; % make sure be row
d = length(mu);
% Get Cholesky factorization of covariance.
R = chol(covm);
% Generate the standard normal random variables.
Z = randn(n,d);
X = Z*R + repmat(mu,n,1);
X = X';
 |
| Two 2-D Gaussian random variables' samples |
10/12/2010
Who bothers with ellipses?
In the previous post, we know how to draw an 2-D ellipse with its center, its major and minor axis, and its orientation. The process can be easily extent to draw N-D multi-dimensional ellipsoid with its center and covariance matrix (of course we can't visualize on N>3).
Now the question is why we need it? Well, mostly for visualization purpose. Check out some following examples.
1. Want to count how many small objects in a given image, such as embryos, and what is their average size?
 |
| Given image with small embryos (and a dime for real area reference) |
Ask my 3-yrs-old daughter to do it - she can count up to 10 :). Or write a simple image processing program, and here I show the result:
 |
| Detect each embryo, fitting by an ellipse, compute its area |
 |
| Elliptic-Shape Clusters in 2-D |
 |
| Ellipsoid-Shape Clusters in 3-D |
One who interested in the image processing or clustering techniques used in these examples can give me a note.
Any other thoughts? Comments are always welcome.
10/10/2010
Simple code to draw a 2-D ellipse
Sometime you want to add ellipses to your figures or images in Matlab? Rather than update to Matlab 2010 or buy PDE toolbox, you could google around and hopefully you find here: A simple code illustrates how you can do it.
Content
Rotate to derised angle
Move to derised location
Next post will present some examples of "real application" visualization with the help of ellipses.
Any thoughts or comments will be appreciate!
Content
Input parameters of 2-D ellipse
clc, clear, close all x0 = 3; y0 = 3; % Center of ellip a = 2; b = 1; % Major and minor radius phi = 30; % Orientation (degree) num = 100; % #points -> smoothness
draw 'ellip = scaled circle' at origin
theta = linspace(0,2*pi,num); p(1,:) = a*cos(theta); p(2,:) = b*sin(theta); figure(1), hold on plot(p(1,:),p(2,:),'k--','LineWidth',2) axis equal
phi = phi*pi/180; % deg->rad % Rotation matrix: Q = [cos(phi) -sin(phi) sin(phi) cos(phi)]; p = Q*p; plot(p(1,:),p(2,:),'g--','LineWidth',2) plot(0,0,'r+')
p(1,:) = p(1,:) + x0; p(2,:) = p(2,:) + x0; plot(p(1,:),p(2,:),'LineWidth',2) plot(x0,y0,'r+')
Any thoughts or comments will be appreciate!
Subscribe to:
Posts (Atom)